
Winnipeg, Manitoba, R3C 3V4 Canada
Abstract. Multiple linear regression techniques and seven years of data were used to build a biometeorological model of Winnipeg's mean daily levels of Culex tarsalis Coquillett. An eighth year of data was used to test the model. Hydrologic accounting of precipitation, evapotranspiration and runoff provided estimates of wetness while the warmness of the season was gauged in terms of the average temperature difference from normal and a threshold antecedent temperature regime. These factors were found to be highly correlated with the time-senes of Cx. tarsalis counts.
The impact of mosquito adulticiding measures was included in the model via a control effectiveness parameter. An activity-level adjustment, based on mean daily temperatures, was also made to the counts.
This model can, by monitoring the weather, provide forecasts of Cx. tarsalis populations for Winnipeg with a lead-time of three weeks, thereby, contributing to an early warning of an impending Western Equine Encephalitis outbreak.
Weather may be the single most important factor determining the abundance of Cx.tarsalis in Manitoba (Fraser and Brust, 1976). According to McLintock (1948), two weather conditions must prevail before vector mosquitoes are plentiful enough to transmit WEE in epidemic proportions in southern Manitoba, viz., the average of the mean weekly temperatures must be above normal during the last two weeks of June and the average of the mean weekly temperatures during July and August must be at least 2\'fbC above normal. He suggested that Cx. tarsalis levels depend only indirectly on rainfall because the eggs of this species are mainly found in the more permanent types of standing water. Wood et al. (1979) indicate that during warm wet weather, substantial Cx. tarsalis populations, consisting of overlapping generations, can build up as the summer progresses.
This study investigated the relationship between Winnipeg's mean daily Cx. tarsalis counts and the weather in order to develop a quantitative method of estimating, in advances the magnitude and trends in the vector mosquito's population. This forecast should contribute to an early warning of an impending WEE outbreak. For a description of how Cx. tarsalis counts fit into the multidisciplinary process of assessing the risk of an imminent WEE epidemic in Manitoba, see Eadie (1982).
It is hypothesized that the magnitude and seasonal trends in Winnipeg's Cx. tarsalis (female) population, as represented by the city's counts, could be predicted from time-senes of weather conditions. Hydrological accounting of precipitation, evapotranspiration and runoff provided estimates of 'wetness' while the 'warmness' of the season was gauged in terms of the average temperature difference from normal and a threshold antecedent temperature regime. Multiple linear regression techniques were used to build the biometeorological model. The impact of mosquito adulticiding[1] measures are weather related activity-levels of Cx. tarsalis were included in the predictive model. The biometeorological model is an elaboration of an earlier one by Raddatz (1982)
Winnipeg's mosquito surveillance network, consisting of 19 New Jersey style light traps located in and around Winnipeg, provides a data base of Cx. tarsalis counts extending from 1977 to 1983. An eighth year (1984) of data was used to test the model. Mosquitoes are removed from the traps daily between 8:00 a.m. and noon local time. The years 1977, 1981, and 1983 were WEE epidemic years. Notably, the mean daily counts in 1978 and 1982 exceeded the 1981 values without a WEE epidemic occurring. Relatively few C tarsalis were collected during 1979 and 1980 seasons.
The Cx. tarsalis counts tend to fluctuate significantly from day-to-day. Therefore, seems reasonable to treat these daily variations as 'noise' which masks the season population curve, i.e., the sample time series representing the population. Therefore, the 'noise' was filtered from the sample by averaging the daily counts over one-week periods to produce 'mean daily counts'. The averaging period was not tied to the mosquito generation period as the data had not been partitioned in that manner. One-week periods were chosen because weather data were readily available for comparable time periods. Time-averaging resulted in a stepped time-series which is assumed to represent the magnitude and trends in the Cx. Tarsalis population. That is:

N(i) = time-series of daily Cx. tarsalis counts N(JD) = time-series of mean daily counts with units of counts per day JD = the Julian Day.Peak mean daily counts ranged from a low of 5.1 in 1980 to a high of 406.7 in 1983.
2.2. LEADING AND CONCURRENT WEATHER TIME-SERIES
For the weather and climatological time-series, parameters were chosen from data recorded at Winnipeg's International Airport, which is well within the built-up area of the city:
(i) Precipitation (mm): the week's actual precipitation, P, the week's normal precipitation, Pn, the accumulated precipitation since April 1st, Pa, and the precipitation normally accumulated from April 1st to date, Pna.
(ii) Temperature (\'fbC): the week's extreme daily high, Th, the extreme daily low, Tl, the average daily mean, T, the normal daily mean, Tn, and the difference between daily mean and the normal daily mean temperature accumulated since April 1st, averaged over the number of weeks since that date, Ts.
2.3. ABATEMENT MEASURES TIME-SERIES
The type, extent and timing of the control measures undertaken by the City of Winnipeg Mosquito Abatement Branch were obtained from their Annual Reports. Similar information for the province's aerial adulticiding over Winnipeg, in response to the encephalitis emergencies of 1977, 1981, and 1983, were obtained from Manitoba's Emergency Measures Organization.
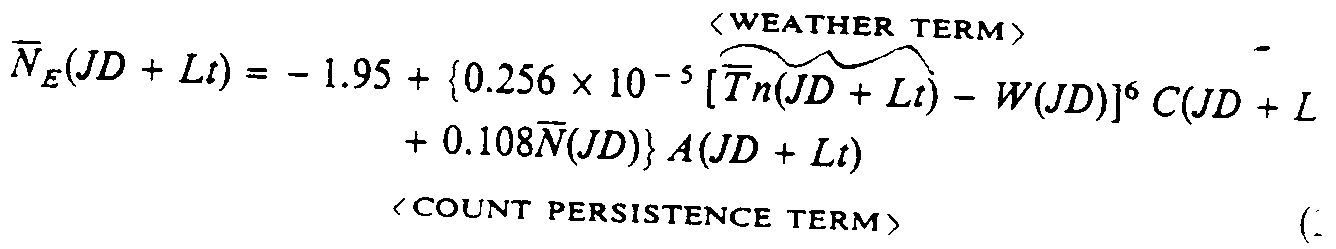
where
JD = the Julian Day
Lt = the lead time of the forecast in days
N}{\f22\dn4 E}{\f22 = the statistical estimate of the mean daily capture-counts with the means calculated over one-week periods ending on the Julian day, JD + Lt
T}{\f22\dn4 n}{\f22 = the normal mean daily temperature for the week ending on the Julian day, JD + Lt
W = a wetness/warmness parameter based on the antecedent weather
C = the control effectiveness parameter
A = an activity-level factor based on the mean daily temperatures concurrent with the counts.
The weather term, multiplied by the control effectiveness parameter and the activity-level factor accounted for 76.8% of the observed variation in the mean daily counts. The count persistence term, multiplied by the activity-level factor. explained an additional 6.7% of the variation. The remaining 16.5% of the variation in the counts was not explained by the model.
3.1 WEATHER TERM
The shapes of the curves, for Winnipeg's seasonal Cx. tarsalis mean daily counts for the dependent sample, roughly coincided with the normal mean daily temperature curve; these curves generally peak in late July. Given that sufficient moisture existed, a persistent period (3 weeks or more) with temperatures at or above a threshold value of 15\'fbC was apparently required to initiate the building of a small spring population into a large summer population. Relatively warm weather with the temperature threshold reached and maintained at an early date, appeared to result in a season with two (possibly more) generations which built to a large peak. Persistent cool weather appeared to restrict the number of generations, resulting in a smaller peak. Insufficient moisture, regardless of the temperature regime, resulted in a small peak, apparently by affecting reproductive activity and/or larval development.
3.1.1 Normal Mean Daily Temperatures, Tn (JD + Lt)
The mean daily temperature is the average of the daily means (i.e.. average of the daily maximum and minimum temperatures) calculated over a one-week period. The normal based on the 42-yr period from 1939 to 1980, were rounded to the nearest degree and adjusted upward slightly to produce a sharp peak at 22\'fbC rather than the actual flat peak at 21\'fbC.
3.1.2 Wetness/Warmness Parameter, W(JD)
This weather parameter was based on both the antecedent moisture and temperature conditions. W(JD) was assigned a value from curve W}{\f22\dn4 1}{\f22 , W}{\f22\dn4 2}{\f22 , W}{\f22\dn4 3}{\f22 or W}{\f22\dn4 4}{\f22 (Figure 8) based on the amount of water retained on or within the ground. i.e., the moisture reserve, R(JD). The choice of the curve was based on the warmness of the season to date and a threshold temperature regime.
The moisture reserve term was tabulated by a method of hydrological accounting developed by Thornthwaite (1944). Incoming water from precipitation is balanced by the outflow of water by evapotranspiration and runoff. Spring start-up values consisting of fall soil moisture storage and winter snowpack, were supplied by an annual ledger which was tabulated on a monthly basis. For the April through August period, the accounting was done on a weekly basis and the moisture reserve was defined as:
R(JD) = 3.0 + S(JD) + D(JD). (3)
The soil moisture storage, S(JD), must always be less than or equal to 100 mm, the water holding capacity, WHC, assumed for the upper soil layer. Surplus water which remained after the evapotranspiration needs were met and soil storage was at capacity was available for runoff. The loss is not immediate for it takes time for water to percolate downward to the water-table to emerge again in streams and rivers. Therefore, only a fraction of the moisture surplus was runoff each week, the remainder staying as surplus. Half of this surplus was assumed to reside in surface depressions, D(JD), whereas the other half was allotted to sub-surface layer storage. When the mean daily temperature for a week was less than -2\'fbC, precipitation was stored as snow and there was no runoff. At higher temperatures, the fraction of the surplus runoff each week was proportional to the runoff coefficient, RC. That is:
Runoff = Surplus/2 x (Number of days in month/RC) (4)
The runoff coefficient, was set at 20 for a one-week melt period resulting in about one third of the spring surplus going into runoff. RC was then sharply reduced to 1 for the summer. When the weekly precipitation exceeded the potential evapotranspiration, increasing outflow from depression and sub-surface storage, the runoff coefficient was again raised. It was assigned a value of 10. When the soil was near saturation. S(JD) > 90 mm, it was set to 20.
Potential evapotranspiration, PE, the amount of water that would be evaporated and transpired from a surface covered with vegetation if there is sufficient water in the soil, was calculated by the Thornthwaite and Mather (1955) method. This procedure requires only actual and climatological temperature values. During periods when precipitation, P, was equal to or greater than PE, the actual evaporation, AE, reaches the potential. When P < PE, moisture was extracted from the soil in amounts which decrease as the oil dries out. The total AE was approximated as follows:
AE = P + S\{[2 x WHC + (P - PE)]/[2 x WHC - (P - PE)] (5)
The choice of the water balance approach outlined above was based on its simple data requirements. The deficiencies of the method are well recognized and it was not expected to produce absolute estimates of the derived components. This was not a major concern as only relative values were needed for input to the regression technique employed in this study. Nevertheless, as a check on the procedure, the computed runoff was compared to the gauged runoff on Sturgeon Creek, a stream whose drainage basin partially over-laps Winnipeg. The parameters used in the water balance calculations were adjusted through trial and error until reasonable agreement was reached. Runoff amounts for the snow-melt period (March plus April) were plotted and show relatively good agreement (Figure 9).
For all the wetness/warmness curves (Figure 8) the greater the moisture reserve. R(JD), the smaller the value of W(JD) and the higher the forecast mean daily count. The series of curves, W}{\f22\dn4 1}{\f22 to W}{\f22\dn4 4}{\f22 , based on the warmness of season to date and a threshold temperature regime, serve as proxies for the stage of the seasonal population build-up. The logic employed in choosing the curve is illustrated in the decision tree (Figure 10)
3.2 CONTROL EFFECTIVENESS PARAMETER, C(JD + Lt)
The control effectiveness parameter was assigned one of three values based on the apparent effectiveness of adulticiding. The influence of larviciding was not included in the model. C took on a value of 1.00, 0.50, or 0.33 based on the occurrence and type of adulticiding. With only 15 of the 19 traps within the control zone. these values correspond to the following:
(i) 1.00 implies that no adulticiding had been undertaken or if undertaken. it had negligible effect on the Cx. tarsalis counts.[2]
(ii) 0.50 or a 50% reduction overall, corresponded to an average decrease in the counts from the traps in the control zone of 65% This value was assigned to weeks when there was ground-based adulticiding. It was also applied to the final week or two of the season, even though no adulticiding took place during these weeks, following the repeated applications of insecticide that occurred in the epidemic years 1977, 1981 and 1983,
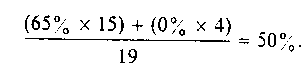
(iii) 0.33 or a 67% reduction overall, corresponded to an average decrease in the counts in the control zone of 85%. This value was assigned to weeks when there was aerial adulticiding.
In the forecast mode, the type of adulticiding, if any, that will be undertaken must be surmised from the magnitude of the forecast count calculated assuming no control.
3 3 COUNT PERSISTENCE TERM, N(JD)
Obviously, mosquitoes reproduce. Therefore, persistence plays a part in determining the size of future counts. However, this term was not of major significa nce because it explained less than 7% of the observed variation in the mean daily counts.
3.4 ACTIVITY-LEVEL FACTOR, A(JD + Lt)
Because the mosquitoes must fly to the traps to be captured, the mean daily counts depend on the activity-level of the population. Experience suggests that warm conditions enhance mosquito flight and biting activity whereas the mosquitoes seem to disappear when it turns cool. The activity-level of the Cx. tarsalis population was partially accounted for by multiplying both the weather and count persistence terms by a factor directly related to the mean daily temperatures concurrent with the counts. This activity-level factor had the following form:
A(JD + Lt) = exp[0.1T(JD + Lt)]/exp[1.5]. (6)
Some example values are given below.
In the forecast mode, Tn can be substituted for T or the long-range (30 day) forecast can be employed to estimate T(JD + Lt).
(Notes)
[1] The application of any insecticide to kill adult mosquitoes.
[2] This latter condition was only invoked once. Ground adulticiding was assumed to have no effect on the mean Cx. tarsalis count for the week ending July 11, 1983. During that week, temperatures were relatively cool; the lowest temperature recorded was 5\'fbC and Cx. tarsalis were just beginning to show up in the trap. This does not imply that the spraying had no effect on other mosquito species.
Eadie, J. A.: 1982. Health Emergency--The Decision Making Process, Western Equine Encephalitis in Manitoba, Manitoba Department of Health, pp. 11-17.
Ellis, R. A.: 1977-1983, Annual Reports, City of Winnipeg, Insect Control Branch, (unpublished).
Fraser, H. M. and Brust, R. A.: 1976. 'Weather Conditions affecting Mosquito Populations in Southern Manitoba During 1975'. Can. J. Public Health, Supplement I to Vol. 67, May/June, pp. 10-46.
McLintock, J.: 1948. 'Report of the Virus Laboratory for 194T, Manitoba Department of Health and Public Welfare, Provincial Laboratories, pp. 161-168.
Raddatz. R. L.: 1982. 'Forecasts of Culex tarsalis Populations in Winnipeg, Manitoba, Western Equine Encephalitis in Manitoba', Manitoba Department of Health. pp. 36-49.
Sekla, L.: 1982, 'Manitoba Arbovirus Surveillance Committee: Description of the Surveillance Program. Western Equine Encephalitis in Manitoba', Manitoba Department of Health. p. 12.
Thornthwaite. C. W: 1981, 'An Approach toward a Rational Classification of Climate'. Geograph. Rev. 38, 55-94.
Thornthwaite. C. W. and Mather, J. R.: 1955, 'The Water Balance', Publications in Climatology, VIII, No. 1, C.W. Thornthwaite Associates, Laboratory of Climatology. Centerton. N J.
Wood, D M., Dang, P T., and Ellis, R.A.: 1979, The Insects and Arachnides of Canada. Part 6, The Mosquitoes of Canada. Diptera: Cuslicadae, Agriculture Canada, p. 380.