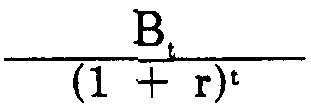
I. INTRODUCTION
[W]e find ourselves forced to hunt for a solution in the dark jungles of the second best[1].
If saving a life is worth spending $1 million today, how much should we spend to save a life in twenty years? The answer, according to the federal Office of Management and Budget (OMB), is $150,000[2]. OMB uses a ten percent annual "discount rate" to convert future regulatory costs and benefits into their "present value."[3] Because government regulation of carcinogens cannot be expected to affect the cancer rate for twenty or thirty years[4], OMB's choice of discount rates has dramatic implications for regulatory policy. Its choice of discount rates has even greater impact on long-term global environmental issues such as ozone depletion and the greenhouse effect[5]. For instance, if the greenhouse effect will cost society $100 billion twenty years from now, OMB's current discount rate would indicate that it is not worth spending $20 billion today to avert the harm.
Significant legal implications also accompany the discounting issue's policy ramifications. In Corrosion Proof Fittings v. EPA[6], the Fifth Circuit invalidated the Environmental Protection Agency's (EPA) carefully considered regulations of asbestos products. Among other objections to the regulations[7], the court found EPA's method of comparing the costs and benefits of an asbestos ban to be unacceptable. The court held that EPA must discount future benefits and that EPA's discounting method gave too much weight to future deaths[8]. Although our discussion concerns more than just toxics regulation, Corrosion Proof Fittings illustrates the significance of the issue not only for policy analysts but also for attorneys.
After several years of review, OMB recently proposed a substantial revision of its twenty-year-old discount policy[9]. Among other changes, OMB proposes increased guidance for government agencies in the use of discount rates in cost-benefit analysis and a reduction of the discount rate from ten percent to seven percent. Coming two decades after the last revision, OMB's current proposal seems an appropriate point to take stock of federal discount rate policy, its underlying assumptions, its impact on environmental policy choices, and its lessons for the coming decades.
This Article attempts to untangle the complex and often obscure debate about the choice of discount rates. It will emphasize the issue of discounting lives, but that issue cannot be readily separated from the broader problem of discounting other regulatory costs and benefits[10]. Thus, our discussion of discounting is also directly relevant to long-term environmental issues such as biodiversity. In particular, most of the same issues arise when cost-benefit analysis seeks to incorporate the intrinsic value placed on the continued existence of an endangered species or other nonhuman lives such as whales or redwoods.
Part II briefly reviews the current role of economic efficiency and cost-benefit analysis in environmental regulation, with particular regard to the problem of assigning a monetary value to human lives. We then explain the basic concept of discounting and demonstrate the momentous impact that choice of a discount rate can have on environmental cost-benefit analyses. Part III explores the debate surrounding the selection of the proper discount rate. Part IV examines questions of fairness to future generations affected by discounting future environmental benefits. Finally, Part V considers how the discounting debate sheds light on the proper uses of cost-benefit analysis.
The discounting issue combines technical economics with philosophical conundrums. Although we will offer suggestions about the proper choice of discount rates, most of our views are necessarily tentative. Nevertheless, one point seems fairly clear: OMB has set its current discount rate too high. This has resulted in an unwarranted curtailment of important environmental regulations.
Before beginning our analysis, it may be helpful for us to explain our general perspective. Essentially, we have attempted to adopt the vantage point of a policymaker in a democratic society, and to ask how such a policymaker should think about long-term programs. Regardless of whether the policymaker uses a formal cost-benefit analysis, she will probably need to understand the trade-offs between environmental protection and economic welfare. Two kinds of trade-offs become especially important for long-term projects. First, money invested in environmental protection might otherwise have been invested in other productive assets. Thus, environmental protection may come at the cost of economic growth. Here, the trade-offs really depend upon whether environmental protection diverts funds from other investments (rather than from current consumption), not on when society receives the benefits. Second, long-term projects produce benefits in the future at the expense of consumption in the present, and the delay may affect how society evaluates the trade-off between current and future welfare. We favor an approach to discounting that treats these factors separately,[11] but even if the decisionmaker adopts a different methodology, we believe she will want to have information about both effects. We have organized our presentation accordingly.
From the vantage point of our (possibly imaginary) thoughtful policymaker, workability is more crucial than theoretical rigor. Economic theorists and professional philosophers rightly concentrate on conceptual nuances and complexities, but the policymaker needs more pragmatic solutions. Furthermore, in a democratic society, the policymaker may have some freedom of action, but also must give weight to the views of the public. For this reason, in evaluating various positions regarding discounting, we have felt free to appeal to what we believe to be generally shared value judgments.
One final introductory point, in the interests of candor. Our belief that the democratic policymaker must give weight to public opinion does not mean government by opinion poll. We believe that our society as a whole, and government in particular, focuses too much on the present and is investing too little for the future[12]. Thus, we think the policymaker should "lean against the wind" a bit, taking a longer view than the latest polls or market reports. Consequently, within the range of positions that seem reasonably supportable, we have leaned toward future-mindedness, which translates into a preference for lower discount rates.
II. A CRITICAL INTRODUCTION TO COST-BENEFIT ANALYSIS AND DISCOUNTING
A. The Role of Cost-Benefit Analysis in Environmental Regulation
Most federal environmental statutes that regulate health risks favor feasibility analysis over cost-benefit analysis[13]. For example, the Clean Air Act mandates the use of maximum achievable control technology to curb emission of hazardous air pollutants[14]. Although numerous provisions of environmental statutes require EPA to consider economic factors, none explicitly requires a formal cost-benefit analysis. Some commentators argue that economic efficiency should have little role in environmental regulation[15]. Nevertheless, in the past decade the federal government has applied cost-benefit analysis increasingly in policymaking, including environmental regulation. President Reagan's famous Executive Order 12,291, promulgated in 1981, requires agencies issuing "major rules" to conduct a cost-benefit analysis to ensure that the benefits of a proposed regulation outweigh its costs[16]. Executive Order 12,291 effectively provides a cost-benefit overlay for all major federal regulatory actions[17]. In Corrosion Proof Fittings, for instance, EPA and the Fifth Circuit independently concluded that the decisionmaking process should include a cost-benefit analysis although the statute does not explicitly require one[18].
More recently, President Bush imposed a ninety-day moratorium on new regulations. During the moratorium, agencies were instructed to existing regulations to ensure compliance with the following standards (among others):
(a) The expected benefits to society of any regulation should clearly outweigh the expected costs it imposes on society.(b) Regulations should be fashioned to maximize net benefits to society[19].
As this executive order illustrates, economic analysis, including efficiency and cost-benefit criteria, is flourishing in federal policymaking. Cost-benefit analysis and its components, including discounting, appear likely to shape environmental policymaking for the foreseeable future.
Valuation is a key step in conducting a cost-benefit analysis. Cost-benefit analysis requires that future benefits be expressed in monetary terms. For goods freely traded on the market, such an assumption is often reasonable. However, for "non market goods" like human life (or the inherent value people place on the existence of other species), the assignment of a monetary value is much more controversial. Even assuming agreement on the propriety of "monetizing" human life, deriving an accurate value is a difficult task. Existing regulations establish values ranging from $70,000 to $132 million per life saved[20]. This tremendous range attests to the difficulty of assigning a specific monetary value to human lives saved. Similar problems hinder efforts to establish a value for the continued existence of an endangered species apart from the species' direct usefulness to humans[21].
When economists talk about placing a value on a human life, they are referring to a statistical life, not to the value of the life of any particular individual. Such valuation essentially attempts to measure what preventing the death of an unidentified person (a "statistical death") is worth to society[22]. Economists suggest several alternative methods for assigning a value to a life saved by regulation, including measures of discounted lifetime consumption, human capital (sometimes called the discounted lifetime production approach), net contribution to society, jury awards in compensation for death, and willingness to pay[23]. Each approach is open to criticism, but economists generally agree that willingness to pay is the best measure[24].
Economists generally use two methods to estimate society's willingness to pay to preserve a life. The first is to use wage differentials between risky and safe occupations to determine the increase in earnings that individuals demand for an incremental increase in risk. That increment can be extrapolated to determine the value workers implicitly place on their lives. A second method--which can also be modified to measure the value placed on endangered species or other aspects of nature--is simply to ask individuals what risk premium they require, using a "contingent valuation" survey[25].
Even assuming that we can estimate accurately what individuals are willing to pay to save a life, the use of such an estimate presents troubling difficulties. Most obviously, willingness to pay depends on ability to pay. Wealthy individuals and groups may be "willing" to pay substantially more for an increment of risk reduction than poor individuals[26]. Further, individuals may inaccurately estimate risk and incorrectly respond to these risks in terms of wage demands for a variety of reasons, including incomplete information, other market imperfections, and misperception of risk[27].
Another objection to willingness-to-pay as a measure is its dependence on the initial assignment of rights. Generally, people will require a larger payment to relinquish a right than they will pay to acquire that right[28]. In order to determine willingness to pay, the decisionmaker must first decide whether an individual already has a right to the good in question. In the asbestos situation, for example, the policymaker would need to determine in advance whether individuals have a right to a healthful, asbestos-free environment[29]. Similarly, if the government conducted cost-benefit analysis to decide whether to save whales, the result could turn on whether the initial entitlement is assigned to whalers or Greenpeace[30].
Apart from the difficulty of placing a dollar value on life, overall reductions in the levels of human mortality may not fully capture the benefits of toxics regulation. Society also may place importance on other characteristics of risks, such as potential clustering of victims[31]. Moreover, regulations may have important incidental benefits that regulators may have even more difficulty quantifying. Analysts tend to omit these "soft variables" from the analysis[32].
For example, in Corrosion Proof Fittings, EPA's calculation of the benefits of an asbestos ban focused on lives saved by the elimination of asbestos and essentially ignored other benefits[33]. Failure to include benefits like reduced treatment costs and diminished environmental degradation caused a significant underestimation of the benefits of asbestos regulation. While EPA mentioned potential illness-and-treatment costs avoided, it failed to include them in its cost-benefit calculation[34]. Similarly, though it acknowledged that an asbestos ban could produce significant ecological benefits, EPA declined to consider such advantages because it found them too difficult to quantify[35]. TSCA protects not only human health, but also the environment[36]. EPA failed to explain why it considered environmental benefits too hard to quantify, but was undaunted by the task of quantifying the benefits in terms of lives saved[37].
Even if saving lives is the primary regulatory goal, statistical deaths avoided may provide an inapt measure of the regulation's value. Placing a value on the small reduction in risk of asbestos-related death that would accrue to each individual provides one alternative to the statistical-deaths-avoided approach. Summation of all individual benefits would yield the total social benefit. Such a measure avoids some of the problems presented by placing a value on life (for example, the distortion involved in extrapolating from small risks valuations to an estimate of the value for certain death) and may more accurately reflect the actual impact of the decision[38]. On the other hand, reliable information on these valuations seems difficult to obtain. The degree to which individuals discount future health effects provides an important determinant of individual valuation of risks. This, however, simply returns us to our central concern, the problem of determining an appropriate discount rate.
B. An Introduction to Discounting
The basic principle underlying discounting is simple: A dollar today is worth more than a dollar at some time in the future. This is the same "time value" principle that underlies the concept of interest. Suppose lender L loans borrower B $100 in year one, to be repaid in year two. L will forego current use of the $100 only if B pays her a premium for that forgone use when B repays the loan in year two. That premium is interest. If B and L agree that B will pay $110 in year two for the use of L's $100 in year one, the simple interest rate is ten percent[39]. If we asked L how much $110 in year two is worth to her today, she would presumably answer "$100." L "discounts" the money she will receive in the future by ten percent. This reflects the time value of money principle: X dollars one year from now is worth less than X dollars today.
The term "present value" describes the current value to the recipient of a benefit that will be conferred in the future. In the above example, the present value to L of $110 in year 2 is $100. The ten percent rate L uses to discount the money she will receive in year two is called the "discount rate." Note that this analysis also applies to costs to be incurred in the future. Everything else being equal, L would be indifferent between paying a cost (for example, a tax) of $110 in year two or $100 today, because L discounts future costs at a simple rate of ten percent per year.
The arithmetic becomes more complicated when more than one period is involved. As money or monetary costs are conferred further in the future, compound interest decreases their present value geometrically. The formula for determining the present value of a sum to be conferred in some future year is:
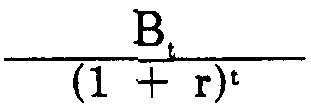
where Bt represents the amount that the beneficiary will receive in future year t, r stands for the discount rate, and t represents the number of years from the present when the beneficiary receives the money[40]. By substituting the monetary value of the benefit for Bt, one can use the above formula to determine the present value of any future benefit that can be expressed in monetary terms. Analysts similarly can discount future costs expressed in monetary terms to present value[41].
The costs and benefits of a given government policy often extend over more than one year. A policy generally distributes those costs and benefits unequally over time, so simple comparison of gross costs and gross benefits would ignore the time value of money. Consequently, cost-benefit analysts generally discount all costs and benefits to present value before comparing them. The difference between the present value of all benefits and the present value of all costs of a project or regulation is often called its "Net Present Value" (NPV). A positive NPV (benefits exceed costs) suggests that the government should adopt a regulation and a negative NPV suggests that it should not.
Thus, to determine the NPV, the policymaker must derive a social discount rate that reflects the time value of the stream of costs and benefits for the entire population affected by the regulation[42]. Determination of the appropriate discount rate presents a tremendous practical problem that federal agencies have not resolved uniformly, despite prodding from OMB[43].
Though justification of the discount rate and estimates of its numerical value vary substantially, economists generally agree that cost-benefit analysis requires discounting future benefits and costs to present value. Given this consensus regarding the need for discounting, an understanding of the impact of the choice of discount rate on the results of cost-benefit analysis becomes important. As the Table on the following page illustrates, discounting can dramatically affect the value of a proposed regulation's costs or benefits,[44] depending on the size of the discount rate and the length of time before society realizes the costs or benefits. Because society often incurs the costs of environmental regulation long before the benefits,[45] compound discounting generally has a greater impact in the calculation of the present value of benefits than of costs.
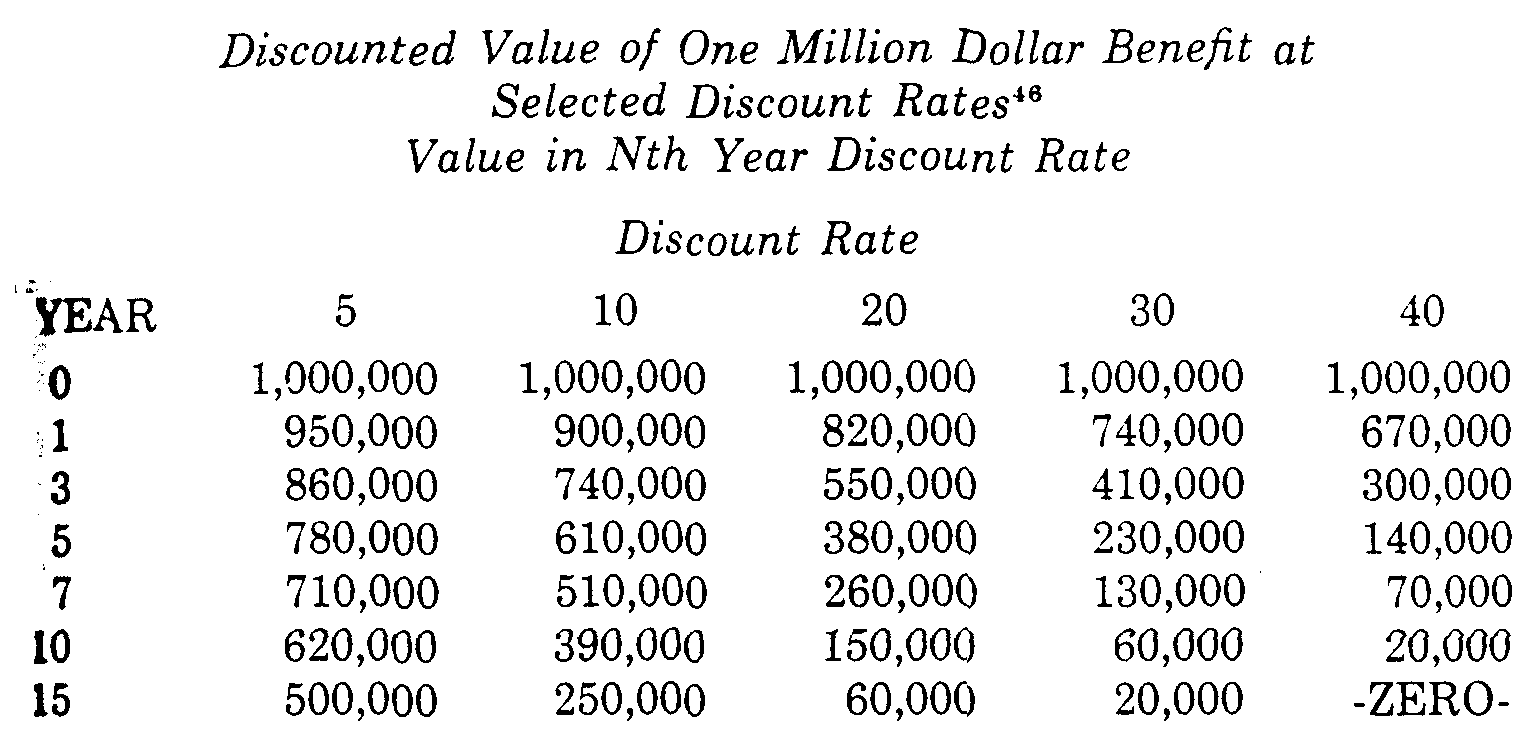
Given these dramatic figures, it should be no surprise that methods of discounting are critical to cost-benefit analysis and often pivotal in regulatory decisions[47].
III. DETERMINING THE APPROPRIATE DISCOUNT RATE
Finding the correct discount rate requires a deeper analysis of why people prefer a given "quantity" of present benefit over the same "quantity" of future benefit. Economists emphasize two explanations: the opportunity cost of forgone benefits, and pure time preference (impatience)[48].
Economists base the concept of social opportunity cost on the productivity of capital. Generally, investment of resources today generates a larger quantity of resources available for future consumption. Thus, the future return from investment (which itself represents forgone present consumption) is essentially a future flow of consumption. The interest rate, and thus the discount rate, reflect the opportunity cost of relinquishing present consumption[49].
The pure time preference principle is grounded mostly in impatience; people prefer receiving benefits immediately over receiving them some time in the future. Economists sometimes call the discount rate derived from this principle the Social Time Preference Rate[50]. Pure time preference also may evidence a belief that future societies are likely to be richer, making an extra dollar of benefit worth less in the future than it is to the current society. Economists often call this rationale for discounting the "diminishing marginal utility" argument. Most economists agree that the discount rate that the time preference explanation suggests--which we will call the social discount rate--is substantially lower than the rate that the opportunity cost indicates[51]. Current estimates, based on the long-term real rate of return on riskless investments (Treasury notes and bonds), are in the neighborhood of one percent[52].
In a world without taxes, the social discount rate should equal the opportunity cost. But the tax system drives a wedge between the two[53]. For example, if individuals use a two-percent discount rate for personal consumption, they will choose to save only if given a two-percent return. But to generate a two-percent return after taxes to consumers, firms must invest in projects offering a higher return. If business and personal taxes take a combined "bite" of fifty percent out of firm income by the time it reaches shareholders, the firm will need to earn a four-percent return in order to give shareholders their two-percent after-tax return. Thus, in this simple example, the social discount rate is two percent, while the implicit opportunity cost of capital is four percent. As we will see, the distinction between the social discount rate and the opportunity cost of capital has crucial importance for cost-benefit analysis[54].
A. Intragenerational Time Preferences and the Social Discount Rate
One rationale for discounting is a simple preference for a benefit today over the same benefit tomorrow. As an empirical observation of psychology, humans are often impatient[55]. However, the issue of whether impatience and preferences based on that emotion are a rational[56] or prudent basis for public policy decisions remains open for debate. Even economists generally agree that time preference provides a weaker justification for discounting than social opportunity cost. Preferences can change over time because of what one commentator describes as a "defect of the telescopic faculty."[57]. For example, a person might express a time preference for saving one life today over ten lives in twenty years, but after the twenty years have elapsed, that same person may favor saving the ten lives. If policymakers discount future benefits based on the aggregate (social) time preference at the time of the decision, they may make decisions that the society will later realize were biased imprudently in favor of small present benefits.
In some sense, saying that future consumption is less beneficial than present consumption is clearly wrong. We may currently place a lower value on the right to drink a milkshake a year from now than on drinking one today. But this does not mean that when we do drink the milkshake, it will taste any worse (or have any fewer calories). Moreover, leaving a milkshake in the freezer for a year will not result in 1.02 milkshakes at the end of the year; milkshakes, like human lives, do not compound. Discounting future consumption on the basis of time preference simply reflects the fact that most people would rather drink a milkshake now than wait a year. Applying the same interest rate to harmful events like deaths implies a preference for postponing pain. Whether these preferences have any rational basis is unclear, even when ordinary consumer goods are involved, let alone human lives or endangered species[58].
Quite apart from concerns about the rationality of individual time preferences, deriving a discount factor from individual behavior is not easy. According to economic theory, rational individuals should use a single discount rate for both saving and borrowing over all time periods. The empirical evidence indicates a quite different result. Riskless investments provide a very low real rate of return, approximately one percent or so[59]. On the other hand, people are willing to borrow money at significantly higher rates, even while maintaining low-interest investments[60]. They also seem to discount future gains differently than future losses, contrary to conventional economic theory[61]. Sometimes, people even will pay money in order to save, as in the once-popular Christmas clubs. These clubs offered the opportunity to lock up funds with no interest (meaning a real loss of value, given inflation), so that individuals would have them available during the holiday season. A desire of people to precommit to various levels of savings seems responsible for least some of these disparities. This desire may make it rational to tie up some funds for a two-percent return while borrowing on a credit card at a much higher real rate[62]. As Professor Lind explains:
Recent developments in behavioral economics suggest that it may not be irrational for the individual to keep budgets separated because of problems associated with self-control. The person who regularly raided the children's college fund to pay off consumer debts might soon find that the children had no money for college. The reasoning is essentially the same as that which many people subscribe to when they deliberately don't take more than a certain amount of money to Las Vegas or to a race track[63].
Turning specifically to discount rates for human lives, a recent survey conducted by economists at Resources For the Future asked a thousand Maryland households about their preferences regarding saving human life[64]. The survey results suggest that, on average, people would discount future lives saved within 25 years at an annual rate of 8.6%, but would use an annual rate of 3.4% if the time horizon is 100 years[65]. A Swedish study using a different methodology found much lower rates, in the neighborhood of .0001 percent[66]. Responses to such surveys vary remarkably. In one study, about ten percent of the respondents had negative discount rates,[67] while many others had (in effect) infinite discount rates: they refused to give any weight to deaths occurring many years in the future, on the ground that science would surely discover a method of eliminating any risk in the meantime[68]. Adding to the confusion, an econometric effort to determine how much people discount their own lives in the future derived a rate of about two percent, close to the return on riskless investment.[69]
Even putting aside the additional perplexities of intergenerational effects,[70] these studies provide few clear answers. Economic theory assumes a degree of consistency regarding intertemporal preferences that seems questionable in the real world. There are also genuine normative concerns about this kind of discounting. Nevertheless, we believe that, with respect to intragenerational effects, policymakers should use a small discount rate in the neighborhood of one or two percent[71]. Although we do not claim that this position is logically unassailable, it is supported by several pragmatic considerations.
Initially, we do not think that policymakers should set the social discount rate higher than the real rate of return on riskless investment, for several reasons. Setting the social discount rate higher than the riskless investment interest rate would imply that the population currently saves too much. (If people save at two percent interest, but discount their own future consumption at a higher rate, they are irrationally trading current consumption for a level of later consumption that they actually regard as less valuable.)[72] This implication about savings is contrary to a broad consensus among economists and the public that American savings rates are actually too low[73]. To counter this hypothetical excessive saving, the government should then run the deficit as high as possible, borrowing money at the riskless rate from foreign investors in order to finance a current spending spree. Although that fiscal policy bears an unfortunate resemblance to government actions during the 1980s, we doubt that the idea of drastically increasing the deficit would find much support[74]. This suggests that in setting the social discount rate the government should act as if the current savings rate were either optimal or too low, not as if it were too high.
Moreover, as we have seen, empirical studies show that people use a variety of discount rates in different situations. Among these rates, the return on riskless investments is arguably the most relevant. Unlike some of the empirical studies of how people would make hypothetical choices, investment rates reflect actual decisions, and therefore indicate preferences more accurately. As compared with many borrowing rates (such as those on consumer credit), investment rates are less likely to reflect impulsive decisions and are more likely to reflect thoughtful deliberation. They are also more likely to reflect long-term preferences, as opposed to short-term desires for liquidity or other effects, such as the practical unavailability of certain goods except on credit (e.g., equity ownership of housing)[75]. Finally, individuals seem to privilege their long-term investment strategies, even when this requires rather expensive efforts to protect against shorter-term impatience. This suggests that investment returns reflect their considered judgment about time preferences better than interest rates on consumer debt.
The preceding discussion suggests that policymakers should not set the social discount rate for intragenerational effects at a higher rate than the real rate of return on investments. Should they set it lower? Although the question probably has more theoretical than practical significance,[76] it is not easy to resolve. The idea of a zero rate has substantial appeal, since a death today and a death tomorrow are in some fundamental sense equal. Nevertheless, we tentatively reject use of a zero discount rate for two reasons. First, we are dealing here only with discounting within a particular generation, not with obligations to later generations[77]. This means that the same individuals are involved in both relevant time periods. The question is whether, in considering costs or benefits to a particular individual, the government should apply a lower discount rate than that individual herself applies in reasonably well-considered personal decisions. Such a policy would raise concerns about paternalism, which at least puts the burden of proof on the proponents of a zero rate.
Second, setting the discount rate at zero would leave it below the rate of return on riskless investments such as government bonds (which also supplies the discount rate for ordinary consumption)[78]. This disparity creates the possibility of paradoxical results. For example, precommitting to future regulations can become optimum for society even though the regulations are never worth their cost[79]. It seems perverse that society should precommit to adopting a regulation that society finds unwarranted today and will find equally unwarranted when it finally goes into effect.
Thus, we believe that policymakers should use the riskless investment rate as both a ceiling and a floor for the social discount rate. According to the most recent empirical evidence, this translates into a discount rate of roughly one percent[80]. Accordingly, in considering intragenerational effects, we should discount future lives, but only at a very low rate.
B. How Should Policymakers Assess Opportunity Costs?
In the previous section, we were primarily concerned with the intertemporal preferences of consumers as a reason for discounting. The fact that dollars invested to comply with regulation might otherwise have been invested provides another justification for discounting future regulatory benefits. Because the investment's benefits (saved lives) remain unrealized for several years, society "loses" the interest on the dollars that it would have obtained if society had employed those dollars elsewhere, earning interest or otherwise appreciating. Discounting accounts for the societal loss of welfare due to foregone investment opportunities[81].
It is important to realize that the opportunity cost rationale applies to the investment in regulatory compliance, not to the value of the regulatory benefits. A life saved today does not earn interest to become two lives twenty years from today. Conversely, if a regulation saves two lives twenty years from today, it makes little sense to say that the opportunity cost of saving those lives means those two future lives are only worth one life today[82]. Similarly, the question of whether full lung capacity and ability to breathe freely at age thirty is any less valuable than the same attributes at age twenty is still open[83].
If adopting a regulation decreases other investment, policymakers should take into account the loss of the possible return from alternative investments[84]. Traditionally, they have done this by using the rate return on alternate investments to help determine the rate for discounting benefits. This method is logically incorrect unless the regulatory benefits and the alternate investments have the same temporal profiles. Essentially, in applying the investment rate of return to regulatory benefits, we are comparing regulatory benefits in the year they accrue with the returns from a hypothetical private investment that would accrue in the same year. This provides a measure of opportunity cost only if the lost opportunity is indeed an investment whose returns will accrue that same year[85].
Because of this problem, economists increasingly have endorsed an alternative method of handling opportunity costs by using a "shadow price" for capital. The idea entails tracing the future returns (including reinvestments) that society loses because a government project or mandated regulatory activity has diverted capital. In other words, the method expresses the opportunity cost as a flow of returns to consumers from alternate investments. The shadow price analysis then reduces this flow to present value; since it is a consumption flow analysis, we use consumer time preferences to determine the discount rate[86].
When analysts subject a government project to cost-benefit analysis, determining the alternate investment return can be quite difficult. It may depend on whether taxes or increased debt fund the projects, whether the government sells its debt abroad or domestically, the time profile of alternate private investments, the marginal propensity of consumers to save, and the extent to which private savings go toward depreciation rather than new investment[87]. Because the results are quite sensitive to initial assumptions, analysts have some concerns about the practical feasibility of this method of discounting for government-financed projects[88].
Fortunately, some recent research and analysis suggests that the problem usually is simpler when the analysis focuses on government regulations as opposed to government expenditures. Because private investments are amortized through depreciation, capital is not withdrawn permanently from the investment pool[89]. Consequently, the analyst needs to account only for the lag between the initial investment and the depreciation recovery. Alternatively, the analyst need only consider the interest payments that are passed on to consumers. Essentially, the question resembles that of determining the economic viability of a new toll road: society needs to compare the benefits received by consumers to the amortized capital costs[90].
The technicalities of determining the shadow price of capital are beyond the scope of this Article. The key point is that the rate of return on forgone private investments relates only to opportunity costs. It is not logically relevant to determining the discount rate for regulatory benefits. Those should be discounted (if at all) by using the social discount rate, which is normally much lower.
IV. EQUITY TOWARD FUTURE GENERATIONS
A. The Scope of Intergenerational Responsibility
Discounting favors regulations that confer benefits in the present or near future over regulations whose benefits society realizes at a later date. One might even say that the purpose of discounting is to favor present benefits over future benefits. Discounting also will generally favor regulations that produce short-term benefits and long-term costs[91]. Even a modest discount rate will favor small benefits conferred today over much larger benefits conferred in the distant future.
A simplified hypothetical illustrates the import of these observations. Assume society is considering two proposals for construction of a nuclear waste repository. For the sake of simplicity, also assume that the two proposals have equal monetary costs, that society incurs those costs in the same year, and that construction of either repository would be completed in a single year. The first option is to build a repository that will last for 500 years, but will almost certainly leak radiation and cause one billion deaths at the end of the 500-year period. Suppose also that we know that the construction of the repository proposed in Option one will result in the loss of no lives. The second option, because of construction hazards inherent in its design, will likely result in the death of at least one, but probably no more than two workers in the year of construction. The second option will not leak in 500 years and thus will not cause any deaths in 500 years. Finally, assume a five percent discount rate.
Although unhappy with the choice, most members of society would probably prefer to save one billion future lives at the cost of one current life, even though society would not receive the benefit for five centuries. However, if a policymaker applied cost-benefit analysis using discounted benefits, she will choose the first option because one billion lives 500 years hence have a lower present value than one life today[92].
Although the above hypothetical is exaggerated, it vividly illustrates how discounting may discriminate against the future[93]. Even in more realistic scenarios, compound discounting often reduces large benefits in the far future to present insignificance. Our previous discussion concerned regulations whose benefits and costs will accrue primarily to the same generation that promulgated the regulation. When a government regulatory decision confers costs or benefits on future generations, additional issues arise[94].
The most compelling questions regarding intergenerational effects of discounting pertain to the rights of future generations and obligations of the present generation to the future. Although philosophical debate about those questions extends beyond the scope of this Article, it is probably safe to assume that most people agree we have at least some responsibilities to consider and provide for the welfare of future generations[95]. Proceeding on that assumption, one facet of the debate about discounting focuses on what discount rate, if any, comports with our responsibility toward future generations. We will begin by briefly canvassing some of the common arguments on the subject.
One argument in favor of discounting benefits to future generations is that, without discounting, the present generation would sacrifice all consumption, because the total benefits to infinite future generations will always exceed any cost to a single current generation[96]. However, that argument proves persuasive only if society intends to maximize net benefits over time, i.e., intergenerational efficiency[97]. Society may also prefer to distribute benefits equitably among generations. If, instead of intergenerational efficiency, society cares about intergenerational equity, it does not need discounting to protect the legitimate interests of the present generation against the claims of the future[98].
An intermediate position might attempt to integrate the goals of efficiency and equity. One possibility is for society to discount future benefits but limit the total discount that it could apply to any future benefit. This method would prevent discounting from diminishing benefits below a certain level and avoid the kind of trivialization of distant future effects epitomized in the nuclear waste repository hypothetical[99].
Another argument that supporters of discounting future benefits sometimes advance is that future generations will be wealthier; thus, our descendants will value any marginal unit of benefit less because it will represent a smaller portion of their total wealth. That "diminishing marginal utility" argument provides little support, however, for discounting future lives saved by regulation. The assumption that future generations will have greater wealth seems somewhat less assured today than as recently as thirty years ago. Even assuming that present conditions justify such optimism, little evidence exists of an inverse relationship between wealth and the value accorded to life and health. The reverse is probably true: future generations may place a higher monetary value on human health relative to other goods if their standard of living increases[100]. The higher environmental, health, and safety standards in wealthy developed countries suggest that such a relationship exists between societies in the current generation[101].
We do not find any of the conventional arguments strongly persuasive. Without pretending to provide a definitive statement regarding duties toward future generations, however, we do think that agreement on some basic points may facilitate progress toward a practical solution.
Because we will appeal at several points to commonly held views about intergenerational responsibilities, we first should clarify what role these conventional views play in the analysis. We believe that in a democratic society, popular values are entitled to prima facie acceptance in public decisionmaking. This does not mean that decisionmakers (whether legislators, administrators, or judges) must slavishly follow public opinion, but only that they should have some adequate grounds for deviation. In particular, when the values in question are as basic as the ones we are about to discuss, decisionmakers should not deviate from those values without strong reasons, which we have not identified in this context. Moreover, because we are dealing with such long-term issues, even a decisionmaker who gives no weight to current public opinion must be concerned with the public's future views. To be sustainable, a long-term environmental program must be capable of maintaining public support over the long haul; otherwise, the program cannot hope to survive long enough to be effective. Of course, decisionmakers may sometimes gamble on the future, hoping that public opinion will shift in their direction. We are skeptical, however, that most people are likely to have a radical change of heart about such fundamental personal questions as their own responsibilities toward their children and grandchildren.
As a practical matter, members of the current generation probably are unwilling to make greater sacrifices for anonymous members of future generations than they are for their own personal descendants. Thus, feelings of obligations toward descendants provide an upward practical bound on obligations toward future generations as a whole[102]. If everyone in the current generation had equal wealth, each would undertake to save enough for her own descendants in order to provide this level of future welfare[103].
With respect to private goods, intergenerational effects raise no special problems because the decisions of individuals to save for their descendants satisfies society's obligation to future generations. As to public goods[104] such as environmental quality, the situation is more complex. Each member of the current generation likely would be willing to sacrifice some current consumption in order to assure his descendants' access to public goods. As usual in public good situations, however, each member cannot do this without providing a free ride--in this situation, to other peoples' descendants. The optimum social decision requires the current generation as a whole to sacrifice the collective consumption needed to provide the desired level of public goods in the future. In other words, with respect to public goods, we can no longer consider each family separately but must consider each generation collectively. However, the objective remains to approximate the level of sacrifice that each family individually would undertake willingly, in the absence of a free ride, to provide the benefits of public goods to their descendants alone. The aggregate of those individual sacrifices would provide the necessary collective sacrifice required of the current generation.
Unfortunately, empirical measurement of the amounts individuals are willing to sacrifice for a future public good would encounter all the difficulties--perception, imperfect information, etc.--inherent in the estimation of individuals' risk and time preferences and individual valuations of human life[105]. These practical measurement difficulties seem to necessitate the use of a proxy measure. As a practical matter, the responsibility to provide for personal descendants probably provides the best benchmark for this generation's obligations to future generations.
This benchmark enables us to invoke some widely shared intuitions. First, whether the language of "moral obligation" is appropriate when considering unborn descendants is not clear. If your great-grand parents squandered the family fortune, you may feel that they acted reprehensibly, but you would have difficulty charging them with violating a personal obligation toward you or with violating a "right" that you possessed. For this reason, we think the language of "responsibility" rather than "obligation" is more appropriate: mature individuals behave responsibly with respect to the interests of their descendants, but do not necessarily owe a "duty" to as-yet nonexistent individuals. Our point is not that the interests of future generations place no constraints on the current generation, but that "rights talk" is a problematic way of discussing the ethical issues.
Second, nothing requires members of the current generation to maximize the income of their descendants, with or without a discount factor. They are not even required to ensure future income levels equal to their own: we would not necessarily consider it irresponsible for extremely rich parents to leave their children only moderately rich. For this reason, the current generation is not truly a trustee with a moral obligation to preserve the entire corpus for future generations[106]. Responsible individuals do attempt, however, to ensure that their descendants can enjoy a decent standard of living, at least if they can do this without extreme self-sacrifice. You would have grounds for complaint if your great-grandparents had taken actions that consigned you to poverty in order for them to live a life of luxury. Again, it might be improper to say that they had violated the "rights" of their future descendants, but they clearly would have acted irresponsibly.
Third, whether or not it is rationally defensible, we think that members of the current generation are felt to have a more compelling obligation toward the next generation (and perhaps at least to young grandchildren) than to later generations[107]. Members of the current generations would be subject to criticism if they did not give the long-term welfare of their children substantial weight; any large discount factor significantly undercuts this responsibility.
Thus, in weighing extremely long-term benefits (more than about one generation in the future), discounting is not a particularly useful technique. This generation's responsibility to later generations seems to involve a side constraint necessary to ensure them a minimum level of welfare, rather than weighing their welfare against our own as part of a maximization problem. As a practical matter. we probably cannot project benefits with even minimal confidence over long periods such as over a century. Even if we could predict some benefits with a degree of accuracy over such long periods, today's generation likely would refuse to make severe sacrifices simply to create marginal improvements in the welfare of distant future generations. We can, however, realistically attempt to avoid substantial risks of future disaster to remote descendants. With few exceptions, these risks will pose dangers to the next generation as well, so our concern for the next generation will usually subsume these very long-term effects.
A maximization approach may have more relevance to decisions affecting the next generation or so, meaning that we might reasonably apply some discount factor. Arguably, we should weigh the welfare of our (collective) children equally with our own. In any event, society cannot set the discount factor too high, since it must accord significant weight to the interests of the next generation. In particular, the discount rate even for economic benefits cannot significantly exceed the expected long-term rate of economic growth; otherwise, we would discount even the destruction of most future Gross Domestic Product to a low present value over periods of only decades[108]. Practically, these considerations require a discount rate no greater than one or two percent.
B. Intergenerational Opportunity Costs
So far, we have been concerned about the problem of discounting benefits that future generations will experience. As we stressed above, this is a separate problem from evaluating opportunity costs. Lawrence Summers, the World Bank's chief economist, has invoked opportunity costs as an argument for a high discount rate for benefits accruing to future generations:
Each project must have a higher return (taking account of both pecuniary and non-pecuniary benefits) than alternative uses of the funds. Standard public non-environmental investments like sewage-treatment facilities, education programmes, or World Bank transport projects have returns of more than 10%. Most private investors apply even higher "hurdle rates" in evaluating investments, generally 15% or more, because higher-return alternatives are available.Once costs and benefits are properly measured, it cannot be in posterity's interest for us to undertake investments that yield less than the best return. At the long term horizons that figure in the environmental debate, this really matters. A dollar invested at 10% will be worth six times as much a century from now as a dollar invested at 8%. . . . [109]
By this point, the fallacy in Summers's argument should be clear. Using the higher discount rates to measure opportunity cost assumes the actual alternative investments were projects having benefits that compounded over a century. This is unrealistic. If the typical government project has a twenty-year life (and the typical private project probably has a much shorter life) then at the end of the twenty years, consumers may receive a high return on the investment. Often, only a small part of that consumer return will be reinvested voluntarily in a new project because the return from that project will be in a nonmonetary form, incapable of reinvestment in that form. Moreover, the marginal propensity to save is, in any event, far below unity.[110]. Using the more appropriate "shadow price of capital" approach, the proper discount rate that society should use to evaluate a project over the century is much lower than the return on any short-term project.
Although Summers does not directly address this point, he may have in mind a different scenario. The higher discount rate would be appropriate if we could make a binding commitment today to invest in higher return projects (such as those of the World Bank) and to reinvest all of the proceeds of the projects in new Bank projects. The problem is that we cannot make meaningful irrevocable commitments regarding government (let alone private) actions over many decades.
For precisely this reason, environmental investments may offer a useful opportunity for precommitment. We may obtain higher returns for the next generation by making investments today that pay lower annual returns but over longer periods. In this respect, social decisionmaking may properly incorporate some of the procedures used by individuals, who make different investments at different interest rates in the interests of precommitment. Environmental protection may be the Societal equivalent of the "Christmas club," in which this generation invests at low returns simply to protect ourselves from wavering commitments (here, as a collectivity, rather than as individuals). Eliminating carcinogens may be a psychologically appealing savings plan. It also may be easier to protect a rain forest or the ozone layer--which might produce a two-percent annual return over a century at the cost of $1 billion in current consumption--than to give $1 billion to the World Bank now and commit ourselves and our descendants to the progressively larger future contributions to the Bank necessary to reinvest fully all of the benefits of Bank projects. This generation probably could preserve the rain forest more easily than a government fund, because of the forest's vividness as a tangible symbol of the heritage of "capital" passed down between generations. Similar reasoning may justify a "sustainability" requirement, which would require maintaining the world's "stock of natural capital,"[111] as a method of maintaining intergenerational savings.
There is a more general point here. In considering opportunity costs, society should consider only other opportunities that it might actually implement; in short, it should choose among the most desirable of the feasible alternatives. In the interest of environmental protection, people might willingly sacrifice $1 billion of current consumption. This does not necessarily mean that they would desire to pay an extra $1 billion in taxes to finance World Bank development projects, or to save an extra $1 billion for private investment. Instead, absent the environmental regulation, they simply might consume the extra $1 billion. Thus, in considering the opportunity cost of environmental decisions, society must determine which are realistic political and social alternatives.
Returning to the familial context we explored earlier, parents who wish to ensure their offspring's inheritance may have difficulty putting aside savings for this purpose. They may find it easier (though in some sense less efficient) to hold onto some family heirlooms, even though those heirlooms appreciate in value more slowly than some other investments. We suggested earlier that the present generation does not actually act as a trustee for the future; the ethical responsibilities of the present generation are more complex than the trust relationship implies. Nevertheless, in some contexts acting as if members of the present generation are trustees may be useful. A stewardship ethic may function as a way of committing the present generation to savings for future generations in a situation in which society considers it difficult otherwise to carry out long-term plans that it considers ethically desirable. Such a stewardship ethic does not require that this generation give great weight to the interests of distant generations. Instead, it merely requires this generation to maintain its global inheritance intact during its children's lives, leaving it to them to apply the same ethic to their own successors. Like runners in a relay race, society may do best when it concentrates on passing the baton to the next runner, leaving the rest of the race to the succeeding runners.
Some readers may think that this approach is short-sighted because it stresses commitments to nearby generations over those farther into the future. We do not believe that our approach slights the long-term interests of the human race. Our approach concerns planning for the full life-spans of this generation's children. This substantially increases the time horizons typically used by today's politicians[112].
Moreover, we have doubts about the workability of any horizon much longer than the life of the next generation. Motivating individuals to make sacrifices for returns that are delayed much longer than the lifespans of their own children would be very difficult. For this generation to design democratic institutions that would keep a given social program in place for such long time periods would be even more difficult. Thus, as a practical matter any policy choice made today has only a finite period of effectiveness. Finally, even if this generation could "lock in" policy choices for many generations, it probably would choose not to do so. This generation has extremely poor information about long-term policy impacts, and present decisions will undoubtedly require later corrections. Trying to forecast and solve the problems of our distant descendants would be a mistake. The present generation will do well enough if it leaves its successors a livable world and well-designed institutions with which to make their own choices.
We earlier rejected the idea that the current generation is morally a trustee for the overall welfare of future generations[113]. Nevertheless, our analysis suggests that for society to think in terms of a more limited "trust" may be useful. First, the current generation may have difficulty meeting its own savings goals for future generations, and it may be useful to treat aspects of the ecosystem as if they were family heirlooms as a technique of increasing savings. Second, the current generation also has at least a responsibility to leave later generations the minimum requirements for decent lives, which means avoiding any severe, irreparable environmental damage. Depending on the level of sensitivity of the global ecosystem, this may place substantial constraints on current decisions.
V. IMPLICATIONS FOR COST-BENEFIT ANALYSIS
Some advocates of cost-benefit analysis seem to view it as providing an objective, reliable standard for policy decisions. We reject the view that cost-benefit analysis defines the right answer for both normative and practical reasons.
First, at most cost-benefit analysis can show only that the benefits of a policy exceed its costs: that is, the winners could afford to compensate the losers for their losses[114]. This standard can be problematic even when dealing with small policy changes and short periods of time, because it fails to address distributional effects[115]. With larger policy changes--large enough to have ripple effects on prices and out puts--the application of this standard becomes more debatable. No unambiguous way may exist for deciding which of two very different economic states leaves consumers better off[116]. Long time spans compound these effects. The compensation standard becomes fanciful when the question is whether individuals yet to be born would willingly pay compensation (via a time machine?) to today's consumers. Thus, cost-benefit analysis becomes increasingly questionable as a normative standard when the current generation considers choices with global or very long-term impacts.
Notorious questions exist concerning the validity of the willingness-to-pay standard for valuing outcomes. Government regulations often involve risks for which no private market exists. For example, there is no private market in which consumers pay for changes in the carcinogen content of their families' air. Economists estimate the value of those changes to consumers based on other estimates (themselves not very reliable) of what people willingly pay to avoid safety hazards in the workplace. If a market for safe air existed, prices might well diverge from those in the employment safety market. In reality, studies of how people evaluate various risks suggest that prospective employees place importance on many factors other than mortality rates[117]. Thus, the preferences at issue are somewhat hypothetical and assignment of pre-rise values elusive.
This becomes even more apparent when we consider long-term risks. Some researchers have asked people to choose between saving some number of lives today and saving a greater number in the future[118]. We doubt that these results measure some preexisting preference, that in some sense is already present in people's heads. Why should people possess preferences about choices they have never had to make and reasonably can expect to have no future power over? Instead, the responses are simply the efforts of individuals to comment, without very much opportunity for thought, on a hard issue of public policy. In short, they most likely are exhibiting offhand opinions on the same policy issue to which the cost-benefit analyst purports to give his own answer, not private preferences that might be reflected in their own market transactions. Asking people for an instant opinion on an issue is an interesting enterprise, but not a promising method for making hard decisions.
Quite apart from these normative questions, as we have seen, cost-benefit analysis as a practical matter is far from being a determinative technique. The problems we have seen with determining the proper discount rate merely exemplify this. Equally difficult problems persist in determining the proper figure to use for the value of human life or the intrinsic value of living in a world with redwoods, whales, and rain forests[119]. Trying to establish quantitative risk estimates is even more speculative. Because of the severe limits on current scientific knowledge, we often can do little more than make educated guesses about the effects of a chemical on human health or on the greenhouse effect. As a result of these uncertainties, cost-benefit analysis can really only identify a few highly promising projects or rule out extremely poor projects[120]. Most decisions fall into a grey area in which the cost-benefit analysis turns on discretionary technical choices. Hence, cost-benefit analysis can often serve most effectively as a method of triage.
Thus, we reject the view that cost-benefit analysis provides the solution to the problems of weighing various policy options and their ramifications. On the other hand, environmental regulation does involve difficult tradeoffs, and economic analysis, including cost-benefit analysis, can help clarify those trade-offs. For example, establishing the "shadow price" of capital illuminates the extent of total consumption that society sacrifices because of a government regulation or project. Similarly, if we determine the extent to which people demand compensation for safety risks in labor markets, we have at least a starting point in considering the extent to which society should sacrifice to eliminate other risks. And if the question is whether to reduce current consumption for future benefits, examination of private savings rates gives us some guidance. If people are unwilling to save at a zero percent interest rate, the government should not undertake such savings on their behalf without some good reason to believe that private preferences have gone awry. Cost-benefit analysis thus incorporates useful factors, but some times makes the mistake of seeking to turn guidelines and insights into definitive answers.
Our conclusions should not be taken as an attack on economic analysis. On the contrary, economists themselves fully realize the limits of cost-benefit analysis. As Robert Lind has said:
[B]enefit-cost analysis need not and cannot provide precise answers to policy questions. Rather it is a procedure that can provide a crude but highly useful picture of the relative merits of alternative policies. It therefore can be used to identify those investments that are either very good or very bad. Benefit-cost analysis also organizes data that bear on policy decisions and does so in a way that educates us about the important elements of a problem and allows us to test the sensitivity of the decisions to changes in those elements[121].
VI. CONCLUSION
Choosing the proper discount rate seems to be the most esoteric of technical issues. Certainly, perusing a page or two of the dense equations in the economics literature does little to dissipate that impression. But this problem actually involves both fundamental questions about the operation of the economy and profound issues regarding this generation's responsibility toward the future. It would be highly presumptuous for us to purport to provide a definitive resolution to technical issues that divide leading economists or to other problems that are hotly debated by professional philosophers.
On the other hand, real world decisions about public policy cannot await a definitive academic consensus. If policymakers view cost-benefit analysis as a technique for organizing information and clarifying tradeoffs, it becomes less important to settle on a precise figure for the discount rate and more important to understand the policy dimensions of that determination. One of the primary goals of this Article has been to "unpack" the debate over discounting so that readers can more knowledgeably make their own assessments of the proper treatment of future regulatory effects.
In dealing with issues of this complexity, identifying the right answer is often difficult, but ruling out some wrong answers is easier. Unfortunately, for many years, OMB has implemented a defective policy regarding discount rates[122]. As with the deficit,[123] society has been saddled with policies that increase short-term consumption at the expense of long-term welfare. The consequence has been to encourage myopia by regulatory agencies.
We have also tried to articulate a working approach to the issues for use by policymakers. Briefly, we have four recommendations:
(1) Policymakers should discount intragenerational environmental benefits at the social discount rate (one percent or so).(2) They should assess opportunity costs of regulations using the "shadow price" of capital if possible[124].
(3) Society's concern about future generations should focus mostly on the welfare of the next generation, although it should be careful not to expose later generations to serious deprivation (including major ecological damage).
(4) With respect to the next generation, policymakers should use a low discount rate (probably around the social discount rate).
One of the cliches of recent public life has been that our society is "eating its seed corn." We believe that renewed attention to the future is a national priority. In technical terms, this requires a changed approach to discounting.
* Associate Dean for Faculty and Henry J. Fletcher Professor of Law, University of Minnesota.
____________________
1. William J. Baumol, On the Social Rate of Discount, 58 Am. Econ. Rev. 788, 789 (1968).
2. Under its proposed reduction of the regulatory discount rate to seven percent, OMB would calculate the value of a life in 20 years at $260,000. See notes 10 and 122 and accompanying text.
Throughout this Article, we will assume that inflation has been "factored out," so that both interest rates and dollar amounts are given in "real" rather than "nominal" terms.
3. OMB Circular A-94 at 4 (1972). For an introductory treatment, see Zygmunt Plater, Robert Abrahams, and William Goldfarb, Environmental Law and Policy 59-63 (West, 1992). For the neophyte, Part II.B of this Article explains the terms "discount rate" and "present value."
The issue of discounting the benefits of environmental regulation figured to play a prominent role in the confirmation controversy over Supreme Court nominee Douglas Ginsburg in 1987, before Ginsburg withdrew his name from nomination. As chief of regulatory policy at OMB in 1985, Ginsburg reportedly forced EPA to withdraw proposed asbestos bans because the costs of the project outweighed discounted future benefits, including human lives saved. According to a New York Times account. OMB assigned a $1 million value to each life saved by regulation, but due to long latency periods of asbestos-related cancer, OMB fixed the discounted value of the "benefit" of saving a life at only $22,000. A contemporary report by the U.S. House Committee on Energy and Commerce characterized such a calculus as "morally repugnant." Robert Pear and Jeff Gerth, Court choice in Focus: A Portrait of Ginsburg, N.Y. Times A1 (Nov. 1, 1987). More recently, then-Senator Albert Gore, Jr. vigorously attacked the use of discounting. See Albert Gore, Jr, Earth in the Balance: Ecology and the Human Spirit 190-91 (Houghton Mifflin, 1992).
6. 947 F.2d 1201 (5th Cir. l991).
8. Corrosion Proof Fittings, 947 F.2d at 1218. The court made several comments on EPA discounting practices:
i. Because the EPA discounted future costs of the regulation, primarily costs of compliance to asbestos products manufacturers, it must discount future benefits "to preserve an apples-to-apples comparison."ii. The EPA must discount "non-monetary" benefits (primarily human lives saved).
iii. The correct time to discount benefits from elimination of asbestos is the time of injury, not the time of exposure to asbestos used by the EPA. (This is significant because a long latency period generally elapses between exposure to asbestos and the onset of asbestos-related disease).
iv. The EPA must quantify and discount benefits for a period longer than 13 years in the future.
v. "[S]oon-to-be-incurred costs are more harmful than postponable costs."
Id. at 1218-19. For commentary on Corrosion Proof Fittings, see Robert Percival, et al., Environmental Regulation: Law, Science and Policy 565-70 (Little, Brown, 1992).
11. This is the so-called "shadow price of capital" approach. See text accompanying notes 85-90.
14. Clean Air Act section 112(d)(2), 42 U.S.C.A. section 7412(d)(2) (West Supp. 1991).
18. See Corrosion Proof Fittings, 947 F.2d at 1214; 54 Fed. Reg. at 29467 (cited in note 4).
24. See Viscusi, Valuation of Risks at 207 (cited in note 20).
26. Viscusi states the problem and his response:
The richer one is, the safer the job one will select from any given wage-risk schedule that is offered in the market, other things being equal. Society may wish to redistribute income . . . so that people will not find it necessary to increase their income through hazardous work, but in terms of the market choices, these different tradeoffs reflect the preferences individuals exhibit.
Viscusi, Valuation of Risks at 197. This response seems to place excessive reliance on the market, ignoring the tremendous cost (and market distortions) of such redistributional programs in relation to the cost of developing an alternative measure for valuing life.
28. See, for example, Farber, 41 Stan. L. Rev. at 1023-24.
30. See Farber, 41 Stan. L. Rev. at 1023-24.
33. 54 Fed. Reg. at 29485-87 (cited in note 4).
35. 54 Fed. Reg. at 29480, 29486 (cited in note 4).
46. Compound rates from Sassone and Schaffer, Cost-Benefit Analysis at 128 (cited in note 42).
50. Pearce and Turner, Economics of Natural Resources at 213 (cited in note 48).
55. See Jonathan Baron, Thinking and Deciding 438 (Cambridge, 1988).
64. We have some doubts about the meaningfulness of these surveys. See text accompanying note 118.
68. Cropper, Aydede, and Portney, 1991 Am. J. Agric. Econ. at 1411, 1412, 1415.
78. For the government to devote resources--or require the private sector to devote resources--to a program with a zero rate of return makes little sense. It could have used the same funds instead to reduce the deficit, thereby eliminating a flow of one or two percent annually payable by our taxpayers to foreign investors.
This argument applies even to lifesaving programs. If the value of saving a life is $5 million, at a zero discount rate we would spend the same amount to save a life in 20 years. But if we spent the same amount of money to reduce the national debt, we would receive about a one-percent annual return, adding some interest savings to the $5 million. So the people affected by our decision would prefer that we use the funds to reduce the national debt, decrease their obligations to foreign investors, and not fund the regulatory program.
80. See note 59 and accompanying text.
85. See Lind, Discounting for Time and Risk at 50 (cited in note 53).
91. See Gillette and Hopkins, Federal Agency Valuations at 62 (cited in note 20).
95. Discussions of these issues include Symposium, Agora: What Obligation Does Our Generation Owe to the Next? An Approach to Global Environmental Responsibility, 84 Am. J. Intl. L. 190 (1990); James Woodward, The Non-Identity Problem, 96 Ethics 804 (1986); Derek Parfit, Reasons and Persons at 480 (cited in note 92); B. Barry, Justice Between Generations, in P.M.S. Hacker and J. Raz, eds., Law, Morality and Society 268 (Clarendon, 1977); John Rawls, A Theory of Justice sections 44, 45 (cited in note 56). Much of the debate turns on the problem of how to assess moral duties toward individuals whose very existence depends on our own actions. Adoption of any major social or regulatory program will have at least some effect on people's lives, and hence on whom they marry, the dates of their children's birth, and so forth--all of which means that children will be born who are not identical to those who would have lived without the program. If someone leads a happy life but dies at age 40 because of the program, is she worse off than she would have been if, without the program, she had never been born? If not, can the program violate any moral obligation owed to such members of future generations?
As Professor D'Amato suggests, even minor programs may have substantial effects on the composition of future generations, due to what is called the "butterfly effect" in chaos theory. Anthony D'Amato, Do We Owe a Duty to Future Generations to Preserve the Global Environment? 84 Am J. Int'l L. 190, 192-93 (1990). When choices involve major programs and long timespans, our decisions may change the identity of virtually every member of a future generation.
Although the philosophical issues are intriguing, we agree with Derek Parfit (who first raised the whole problem of "potential persons") that they have little practical relevance. See Derek Parfit, Comments, 96 Ethics 854, 855 (1986).
100. See Merkhofer, Decision Science at 101 (cited in note 25).
104. The key characteristics of public goods are joint supply and nonexcludability, which together mean that everybody essentially consumes the same amount of the good. (Nonexcludability means that preventing individuals from consuming the goods once they are made available is impractical; joint supply means that supplying the goods jointly is more efficient because of declining marginal cost.) National defense and clean air provide classic examples of goods with these characteristics. A government can only supply these goods practicably to the population as whole. See Dennis Mueller, Public Choice II 10-11 (Cambridge, 1989).
To the extent that individuals care about the general future welfare of society, as opposed to that of their own descendants, social welfare itself takes on some of the attributes of a public good. This means that privately determined discount rates may not be appropriate. See Sen, Choice of Discount Rates at 326-37 (cited in note 97).
105. See notes 25-30 and accompanying text.
108. As Professor Lind explains:
Suppose we select a social discount rate based on present consumer rates or the rate of return on investment. Historically, any such rate is likely to exceed the rate of growth of the economy, often by a large amount. Then the basic arithmetic of exponential growth applied in a cost-benefit analysis implies that, regardless of how small the cost today of preventing an environmental catastrophe that will eventually wipe out the entire economy, it would not be worth this cost to the present generation if the benefits in the future are sufficiently distant. To most of us, this would seem a highly questionable if not immoral public policy.
Lind, 18 Envir. Econ. & Mgmt. at S-20 (cited in note 59).
113. See text accompanying note 106.
123. See generally, Symposium on the Budget Deficit, 3 J. Econ. Persp. 17 (1989).